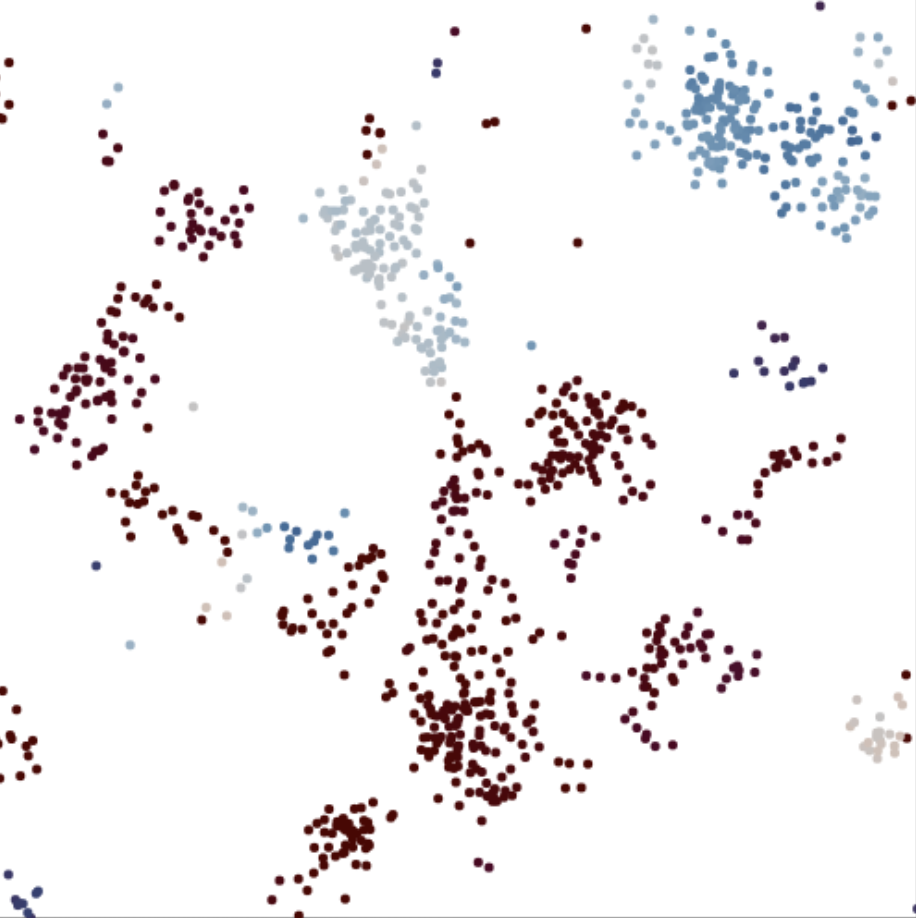
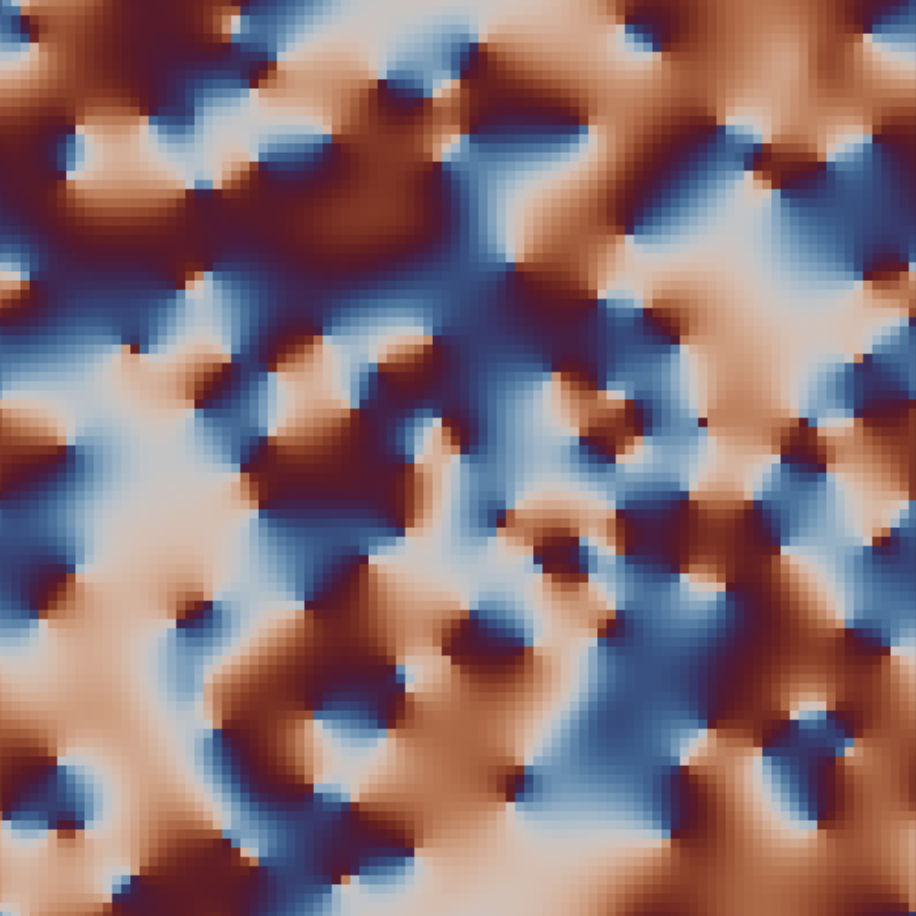
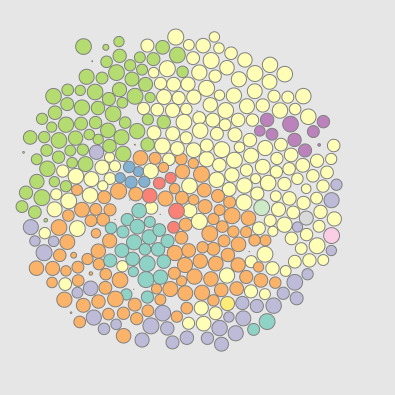
“The Prisoner's Kaleidoscope”
The prisoner's dilemma game on a lattice
This explorable illustrates beautiful dynamical patterns that can be generated by a simple game theoretic model on a lattice. The core of the model is the Prisoner’s Dilemma, a legendary game analyzed in game theory. In the game, two players can choose to cooperate or defect. Depending on their choice, they receive a pre-specified payoffs. The payoffs are chosen such that it seems difficult to make the right strategy choice.
“Horde of the Flies”
The Vicsek-Model
This explorable illustrates one of the most famous and most fundamental models for the emergence of flocking, swarming and synchronized behavior in animal groups. The model was originally published in a 1995 paper by Tamás Vicsek and co-workers and is therefore called the Vicsek-Model. The model can explain why transitions to flocking behavior in groups of animals are often not gradual. Instead, one can expect a sudden emergence of flocking and synchronized movements if a critical density is crossed.
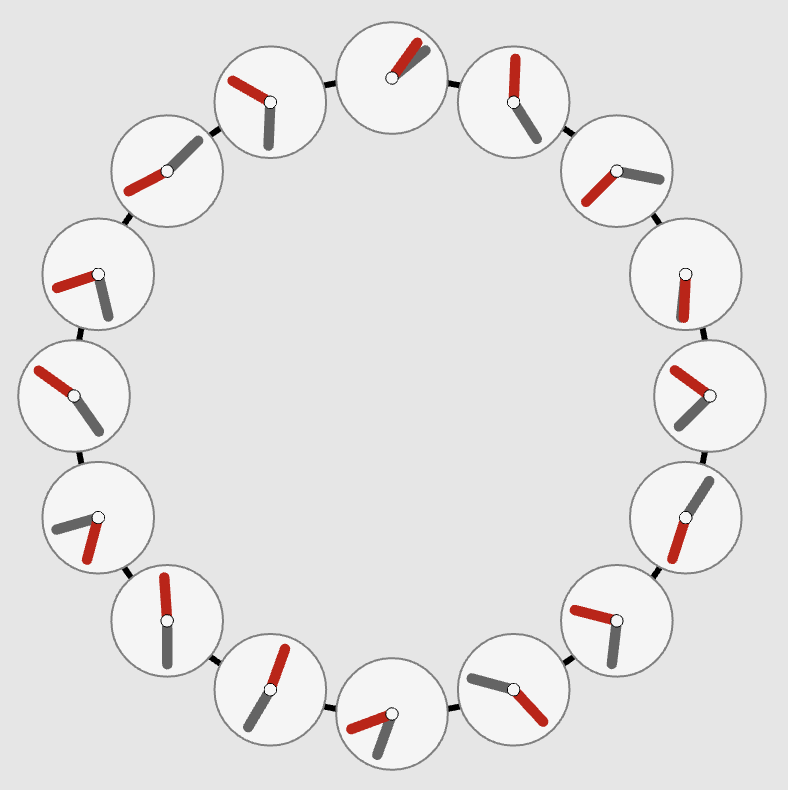
“Spin Wheels”
Phase-coupled oscillators on a lattice
This explorable illustrates pattern formation, interesting and beautiful properties of oscillators that are spatially arranged on a lattice and interact with their neighbors. Oscillators and their interaction are described by the famous Kuramoto Model for phase coupled oscillators. The model is amazing, because on one hand it is conceptually quite simple, on the other it holds a number of unexpected dynamical secrets that you can discover here.
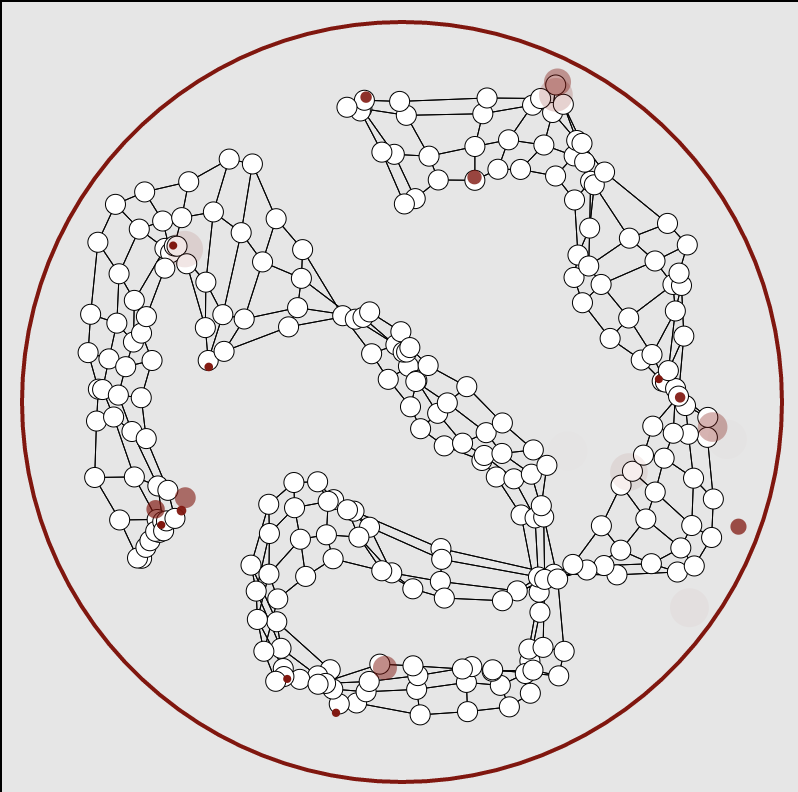
“Eigenartig”
The spatial hypercycle model
This explorable illustrates the dynamics of the famous hypercycle model. It was originally conceived by Peter Schuster and Nobel laureate Manfred Eigen (1927-2019) in 1979 to investigate the chemical basis of the origin of life. Because living things make copies of themselves, in the beginning complex chemicals like polymer chains, including small RNA molecules (see e.g. RNA-world), had to acquire the ability to catalyse their own synthesis from smaller parts, e.g. single nucleotides.
“Swårmalätørs”
Oscillators that sync and swarm
This explorable illustrates how remarkable spatio-temporal patterns can emerge when two dynamical phenomena, synchronization and collective motion, are combined. In the model, a bunch of oscillators move around in space and interact. Each oscillator has an internal oscillatory phase. An oscillator’s movement and change of internal phase both depend on the positions and internal phases of all other oscillators. Because of this entanglement of spatial forces and phase coupling the oscillators are called swarmalators.
“Come Together”
Chemotaxis in Dictyostelium discoideum
This explorable illustrates how simple, single-cell organisms can manage to aggregate into multi-cellular structures by emitting and responding to chemical signals. Individual cells respond by orienting towards a chemical signal and moving up its gradient, a process known as chemotaxis. The combination of synchronized signal emission and chemotaxis yields collective behavior with beautiful spatial branching patterns during the aggregation process.
“Thrilling Milling Schelling Herings”
Swarming behavior of animals that seek their kin
This explorables is a combination of two models, one that explains the emergence of dynamic patterns and collective behavior in schools of fish or flocks of birds, the second, the Schelling model, captures the geographic segregation of populations of different kinds of individuals. When these two models are combined, a great variety of beautiful dynamic swarming patterns can be generated. These patterns show traces of the generic swarming states like “milling” and segregation effects within these dynamic states.
“Repliselmut”
Yet another Complexity Explorable on evolution
This explorable illustrates how variation and selection in a population of replicating organisms naturally leads to a gradual increase in the population’s overall fitness. The explorable simulates a system that is captured (to some extent) by the Replicator-Mutator Equation which is both, a generalization of the famous Replicator Equation and the Quasispecies Equation.
“Janus Bunch”
Dynamics of two-phase coupled oscillators
“Nah dah dah nah nah... (Opus, 1984)”
Conway's Game of Life
“Hopfed Turingles”
Pattern Formation in a simple reaction-diffusion system
With this explorable you can discover a variety of spatio-temporal patterns that can be generated with a very famous and simple autocatalytic reaction diffusion system known as the Gray-Scott model. In the model two substances $U$ and $V$ interact and diffuse in a two-dimensional container. Although only two types of simple reactions occur, the system generates a wealth of different stable and dynamic spatio-temporal patterns depending on system parameters.
“Dr. Fibryll & Mr. Glyde”
Pulse-coupled oscillators
This explorable illustrates pattern formation in excitable media. The example explored here in a system of pulse-coupled oscillators that are arranged on a two-dimensional lattice and interact with their neighbors by delivering excitatory pulses to them and receiving them in return. This model is sometimes used to study synchronization and can capture the dynamics of activation in layers of neurons as well as the spatial patterns of signaling molecules that play a role in microbial aggregation processes.
“Scott's World*”
Microbial growth patterns
This explorable illustrates a dynamic model for pattern formation in a growing community of microbes. Many microbial organisms exhibit collective behavior when a community of them expands say on a surface with nutrients. These patterns are often very beautiful and rich in structure.
“Yo, Kohonen!”
Kohonen's Self-Organizing Map
This explorable illustrates the dynamics of a self-organizing map (SOM), specifically a neural network known as the Kohonen Map. The Kohonen map is a model for self-organization of biological neural networks and how the brain can learn to map signals from an input space, e.g. visual stimuli in the visual field, to a two dimensional layer of neurons, e.g. the visual cortex in the brain, in such a way that neighborhood properties in the stimulus space are conserved as best as possible: Neurons that are neighbors in the neural network should respond to stimuli that are also close in stimulus space.
“Kelp!!!”
A stochastic cellular automaton
This explorable illustrates how fractal growth patterns can be generated by stochastic cellular automata. Cellular automata are spatially and temporally discrete dynamical systems that are conceptually very straightforward but can generate unexpected complex behavior, often fractal-like structures reminiscent of patterns we see in natural systems.
“Surfing a Gene Pool”
Expansion of clones with idential fitness
This explorable is about pattern formation in a model system for the growth of a bacterial population in a petri dish in which the bacterial population is made up of a mix of two or three mutant strains that have identical fitness and reproduction properties. In the model system, an initially well mixed drop of bacteria with an equal amounts of every mutant strain is positioned in the center of the petri dish. After that, the bacteria start replicating, the population expands radially and a pattern will emerge.
“Ride my Kuramotocycle!”
The Kuramoto model
This explorable illustrates the Kuramoto model for phase coupled oscillators. This model is used to describe synchronization phenomena in natural systems, e.g. the flash synchronization of fire flies or wall-mounted clocks.
“Maggots in the Wiggle Room”
The dynamics of evolution
This explorable illustrates an evolutionary process in an “ecosystem” of interacting species (cartoon maggots, in this case). Individuals move around in their enviroment, replicate and eat each other. Optionally, mutations can generate new species. The system is similar to the Explorable A Patchwork Darwinge, only a bit more animalistc and dynamically slightly different. However, for this one here, you need a bit more patience in order to observe interesting effects.
“A Patchwork Darwinge”
Evolution: Variation and Selection
This explorable illustrates how the combination of variation and selection in a model biological system can increase the average fitness of a population of mutants of a species over time. Fitness of each mutant quantifies how well it can reproduce compared to other mutants. Variation introduces new mutants. Sometimes a mutant’s fitness is lower than its parent’s, sometimes higher. When lower, the mutant typically goes extinct, if higher the mutant can outperform others and proliferate in the population. This way mutants with higher fitness are naturally selected.
“Into the Dark”
Collective intelligence
This explorable illustrates how a school of fish can collectively find an optimal location, e.g. a dark, unexposed region in their environment simply by light-dependent speed control. The explorable is based on the model discussed in Flock’n Roll, which you may want to explore first.
“Barista's Secret”
Percolation on a lattice
This explorable illustrates a process known as percolation. Percolation is a topic very important for understanding processes in physics, biology, geology, hydrology, horstology, epidemiology, and other fields. Percolation theory is the mathematical tool designed for understanding these processes.
“Lotka Martini”
The Lotka-Volterra model
This explorable illustrates the dynamics of a predator-prey model on a hexagonal lattice. In the model a prey species reproduces spontaneously but is also food to the predator species. The predator requires the prey for reproduction. The system is an example of an activator-inhibitor system, in which two dynamical entities interact in such a way that the activator (in this case the prey) activates the inhibitor (the predator) that in turn down-regulates the activator in a feedback loop. Activator-inhibitor systems often exhibit oscillatory behavior, like the famous Lotka-Volterra System, a paradigmatic model for predator prey dynamics.
“Critical HexSIRSize”
The stochastic, spatial SIRS model
This explorable illustrates the behavior of a contagion process near its critical point. Contagion processes, for example transmissible infectious diseases, typically exhibit a critical point, a threshold below which the disease will die out, and above which the disease is sustained in a population. Interesting dynamical things happen when the system is near its critical point.
“Flock'n Roll”
Collective behavior and swarming
This explorable illustrates of an intuitive dynamic model for collective motion (swarming) in animal groups. The model can be used to describe collective behavior observed in schooling fish or flocking birds, for example. The details of the model are described in a 2002 paper by Iain Couzin and colleagues.
“Particularly Stuck”
Diffusion Limited Aggregation
This explorable illustrates a process known as diffusion-limited aggregation (DLA). It’s a kinetic process driven by randomly diffusing particles that gives rise to fractal structures, reminiscent of things we see in natural systems. The process has been investigated in a number of scientific studies, e.g. the seminal paper by Witten & Sander.
“Cycledelic”
The spatial rock-paper-scissors game
This explorable of a pattern forming system is derived from a model that was designed to understand co-existance of cyclicly interacting species in a spatially extended model ecosystem. Despite its simplicity, it can generate a rich set of complex spatio-temporal patterns depending on the choice of parameters and initial conditions.
“Epidemonic”
The SIRS epidemic model
This explorable illustrates the dynamics of the SIRS epidemic model, a generic model that captures disease dynamics in a populations or related contagion phenomena.
“Keith Haring's Mexican Hat”
Pattern Formation by Local Excitation and Long-Range Inhibition
This explorable illustrates one of the most basic mechanisms for spontaneous pattern formation: Local excitation and long range inhibition. This mechanism or similar ones are responsible for patterns observed in many natural systems, such as neural tissue, animal fur and spatial heterogeneity in social systems.
“Weeds & Trees”
Lindenmayer Systems
This explorable illustrates how fractal patterns observed in natural systems, particularly structural properties of some plants, can approximately be modeled by simple iterative models. Sometimes these models are refered to as Lindenmayer systems.