“The Prisoner's Kaleidoscope”
The prisoner's dilemma game on a lattice
This explorable illustrates beautiful dynamical patterns that can be generated by a simple game theoretic model on a lattice. The core of the model is the Prisoner’s Dilemma, a legendary game analyzed in game theory. In the game, two players can choose to cooperate or defect. Depending on their choice, they receive a pre-specified payoffs. The payoffs are chosen such that it seems difficult to make the right strategy choice.
“Stranger Things”
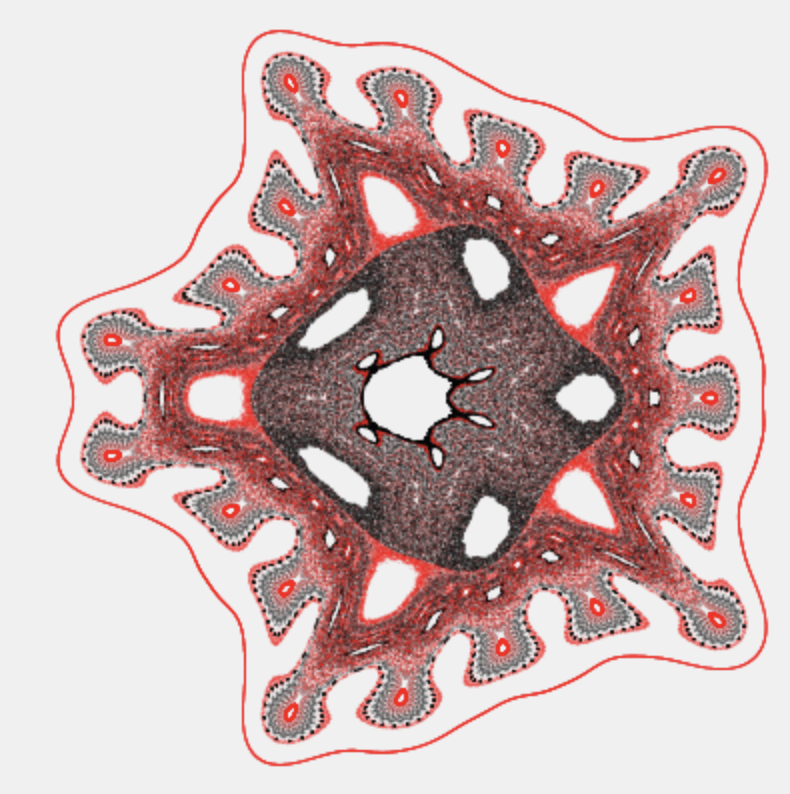
Strange attractors
This explorable illustrates the structure and beauty of strange attractors of two-dimensional discrete maps. These maps generate sequences of pairs of number $(x_n,y_n)$ where the index $n=0,1,2,…$ denotes the step of the iteration process that starts at the point $(x_0,y_0)$. The map is defined by two functions $f(x,y)$ and $g(x,y)$ that determine the point $(x_{n+1},y_{n+1})$ given $(x_{n},y_{n})$:
“Double Trouble”
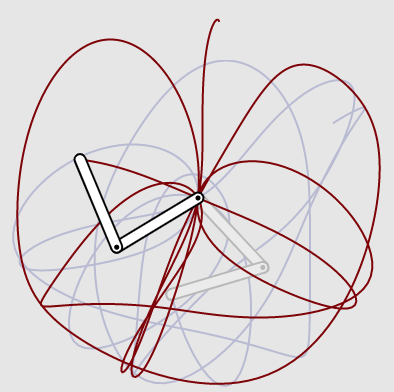
The double pendulum
This explorable illustrates the beautiful dynamical features of the double pendulum, a famous idealized nonlinear mechanical system that exhibits deterministic chaos. The double pendulum is essentially two simple pendula joined by a bearing. It’s a classic complex system in which a simple setup generates rich and seemingly unpredictable behavior. The only force that is acting on it is gravity. There’s no friction.
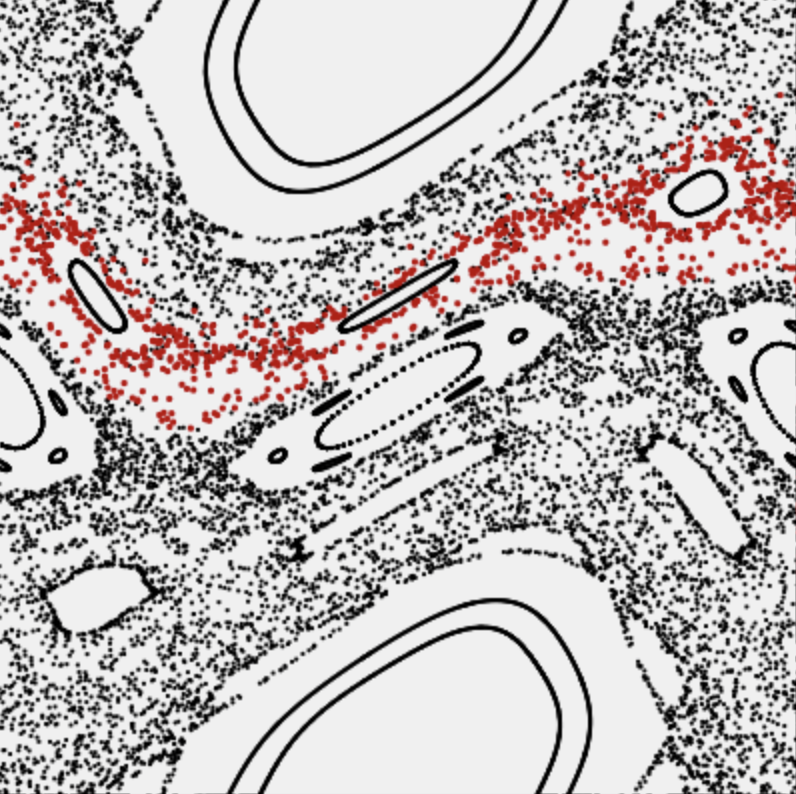
“Kick it like Chirikov”
The kicked rotator (standard map)
In this explorable you can investigate the dynamics of a famous two-dimensional, time discrete map, known as the standard or Chirikov–Taylor map, one of the most famous dynamical systems that exhibits deterministic chaos. It is almost identical to the “Kicked Rotator”, an idealized physical system in which a rotating rod is periodically kicked by an external force.