“Spin Wheels”
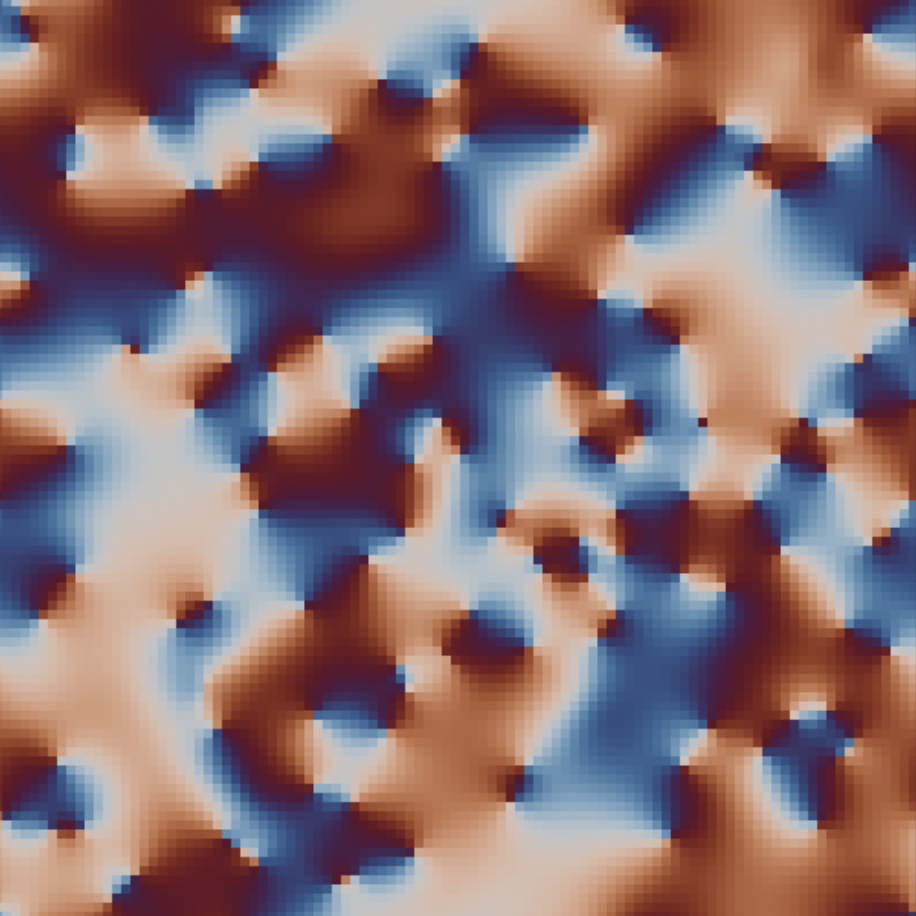
Phase-coupled oscillators on a lattice
This explorable illustrates pattern formation, interesting and beautiful properties of oscillators that are spatially arranged on a lattice and interact with their neighbors. Oscillators and their interaction are described by the famous Kuramoto Model for phase coupled oscillators. The model is amazing, because on one hand it is conceptually quite simple, on the other it holds a number of unexpected dynamical secrets that you can discover here.
“The walking head”
Pedestrian dynamics
This explorable illustrates how a remarkably simple mathematical model for pedestrian dynamics can capture a number of features that are observed in actual pedestrian flows on walkways for example. In the model individual pedestrians move with an individual anticipated speed and direction. When obstacles get in their way, either physical obstacles or other pedestrians, walkers experience a repulsive social force, that alters their velocity and current direction to avoid collision. This alone is sufficient to produce a variety of patterns that are reminiscent of actual pedestrian dynamics. The explorable is a simplified variant of a series of beautiful models introduced by Dirk Helbing that have found a wide range of application, e.g. panic dynamics, crowd turbulence, traffic jams and more.
“Eigenartig”
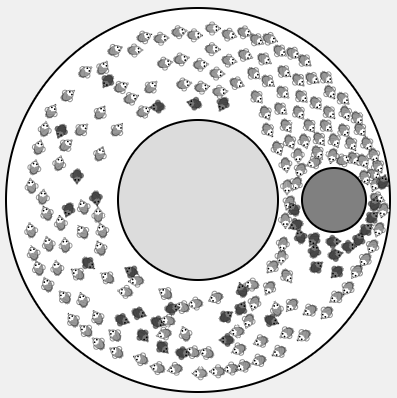
The spatial hypercycle model
This explorable illustrates the dynamics of the famous hypercycle model. It was originally conceived by Peter Schuster and Nobel laureate Manfred Eigen (1927-2019) in 1979 to investigate the chemical basis of the origin of life. Because living things make copies of themselves, in the beginning complex chemicals like polymer chains, including small RNA molecules (see e.g. RNA-world), had to acquire the ability to catalyse their own synthesis from smaller parts, e.g. single nucleotides.
“Swårmalätørs”
Oscillators that sync and swarm
This explorable illustrates how remarkable spatio-temporal patterns can emerge when two dynamical phenomena, synchronization and collective motion, are combined. In the model, a bunch of oscillators move around in space and interact. Each oscillator has an internal oscillatory phase. An oscillator’s movement and change of internal phase both depend on the positions and internal phases of all other oscillators. Because of this entanglement of spatial forces and phase coupling the oscillators are called swarmalators.
“Thrilling Milling Schelling Herings”
Swarming behavior of animals that seek their kin
This explorables is a combination of two models, one that explains the emergence of dynamic patterns and collective behavior in schools of fish or flocks of birds, the second, the Schelling model, captures the geographic segregation of populations of different kinds of individuals. When these two models are combined, a great variety of beautiful dynamic swarming patterns can be generated. These patterns show traces of the generic swarming states like “milling” and segregation effects within these dynamic states.
“Janus Bunch”
Dynamics of two-phase coupled oscillators
“Hopfed Turingles”
Pattern Formation in a simple reaction-diffusion system
With this explorable you can discover a variety of spatio-temporal patterns that can be generated with a very famous and simple autocatalytic reaction diffusion system known as the Gray-Scott model. In the model two substances $U$ and $V$ interact and diffuse in a two-dimensional container. Although only two types of simple reactions occur, the system generates a wealth of different stable and dynamic spatio-temporal patterns depending on system parameters.
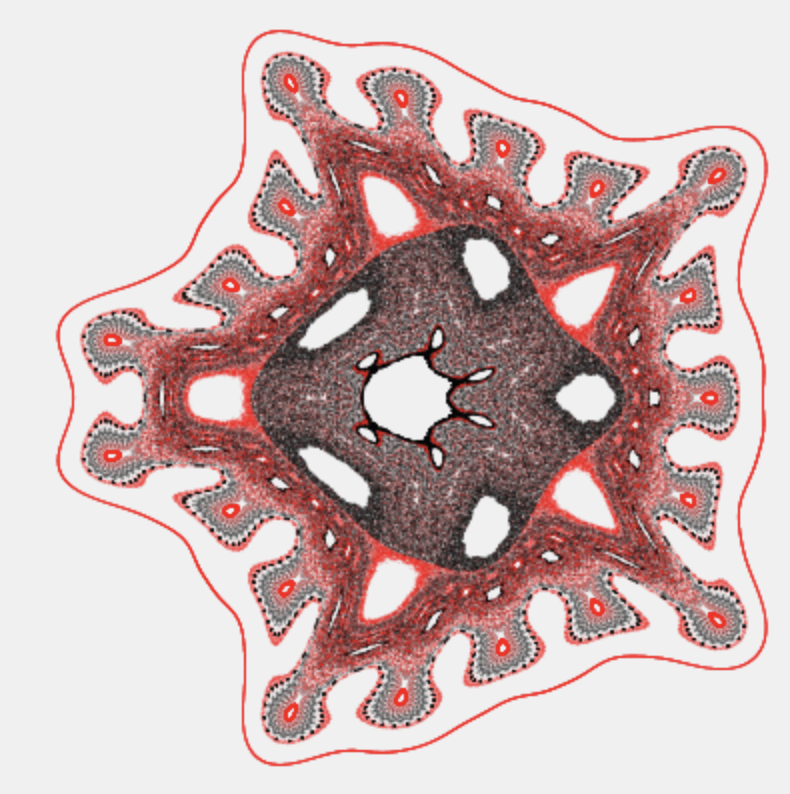
“Stranger Things”
Strange attractors
This explorable illustrates the structure and beauty of strange attractors of two-dimensional discrete maps. These maps generate sequences of pairs of number $(x_n,y_n)$ where the index $n=0,1,2,…$ denotes the step of the iteration process that starts at the point $(x_0,y_0)$. The map is defined by two functions $f(x,y)$ and $g(x,y)$ that determine the point $(x_{n+1},y_{n+1})$ given $(x_{n},y_{n})$:
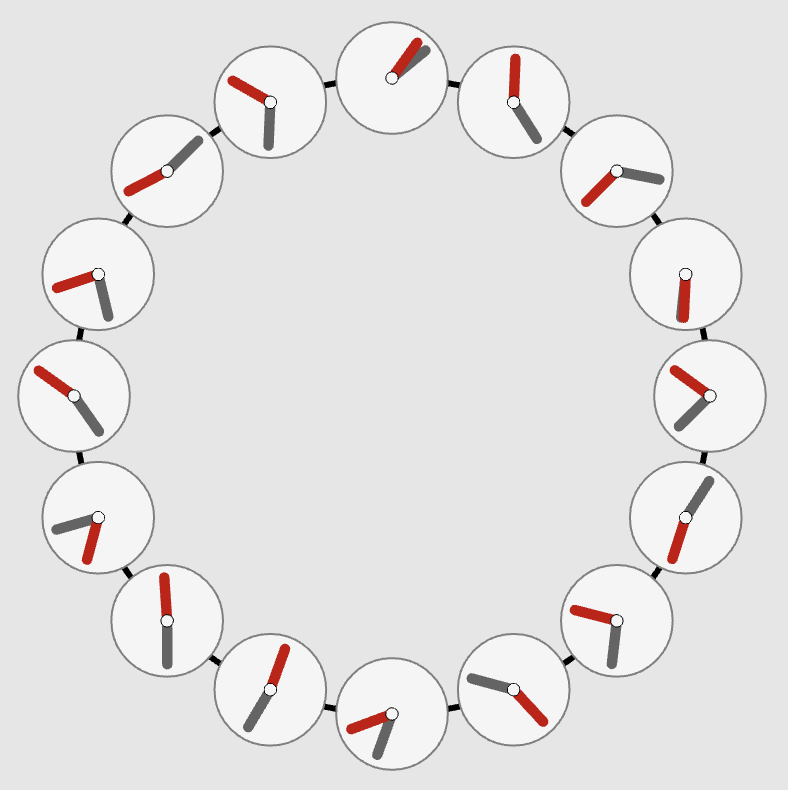
“Ride my Kuramotocycle!”
The Kuramoto model
This explorable illustrates the Kuramoto model for phase coupled oscillators. This model is used to describe synchronization phenomena in natural systems, e.g. the flash synchronization of fire flies or wall-mounted clocks.
“Into the Dark”
Collective intelligence
This explorable illustrates how a school of fish can collectively find an optimal location, e.g. a dark, unexposed region in their environment simply by light-dependent speed control. The explorable is based on the model discussed in Flock’n Roll, which you may want to explore first.
“Lotka Martini”
The Lotka-Volterra model
This explorable illustrates the dynamics of a predator-prey model on a hexagonal lattice. In the model a prey species reproduces spontaneously but is also food to the predator species. The predator requires the prey for reproduction. The system is an example of an activator-inhibitor system, in which two dynamical entities interact in such a way that the activator (in this case the prey) activates the inhibitor (the predator) that in turn down-regulates the activator in a feedback loop. Activator-inhibitor systems often exhibit oscillatory behavior, like the famous Lotka-Volterra System, a paradigmatic model for predator prey dynamics.
“Cycledelic”
The spatial rock-paper-scissors game
This explorable of a pattern forming system is derived from a model that was designed to understand co-existance of cyclicly interacting species in a spatially extended model ecosystem. Despite its simplicity, it can generate a rich set of complex spatio-temporal patterns depending on the choice of parameters and initial conditions.
“Kick it like Chirikov”
The kicked rotator (standard map)
In this explorable you can investigate the dynamics of a famous two-dimensional, time discrete map, known as the standard or Chirikov–Taylor map, one of the most famous dynamical systems that exhibits deterministic chaos. It is almost identical to the “Kicked Rotator”, an idealized physical system in which a rotating rod is periodically kicked by an external force.
“Epidemonic”
The SIRS epidemic model
This explorable illustrates the dynamics of the SIRS epidemic model, a generic model that captures disease dynamics in a populations or related contagion phenomena.