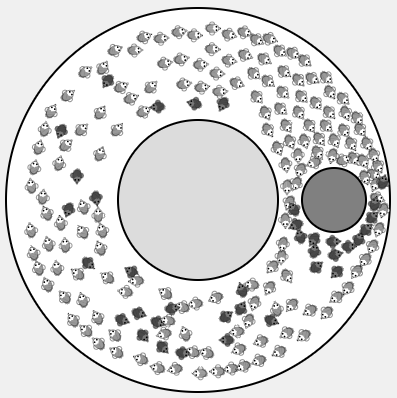
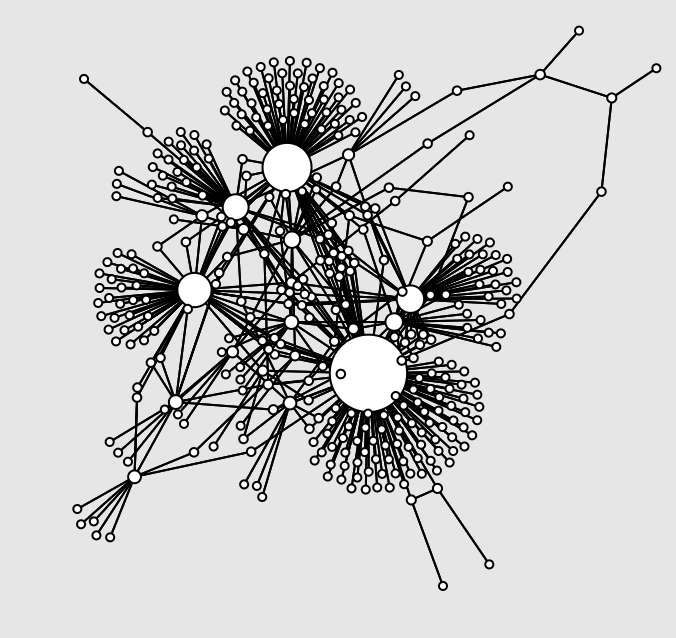
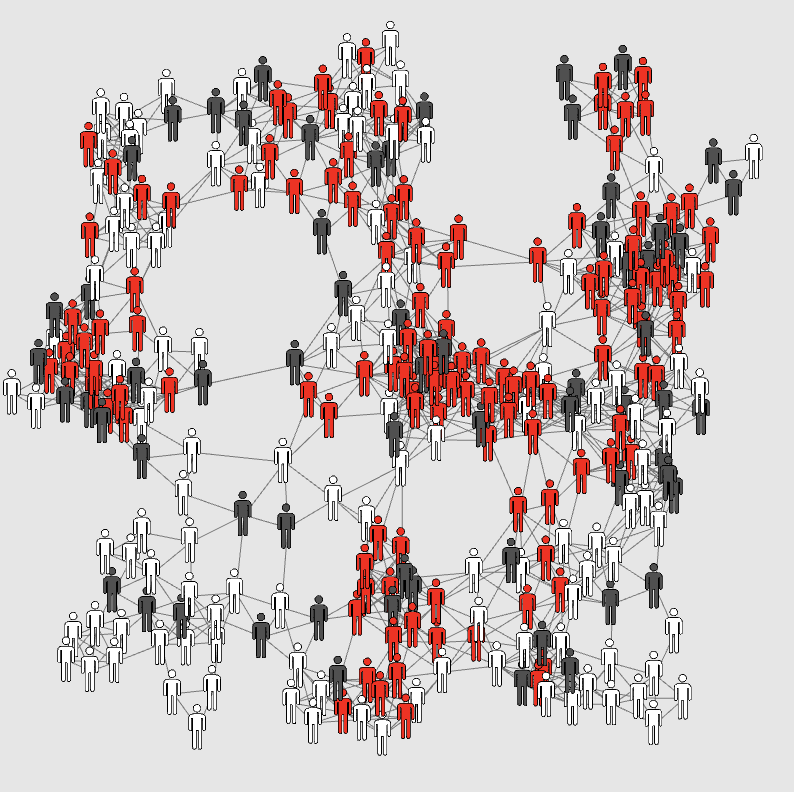
“The Prisoner's Kaleidoscope”
The prisoner's dilemma game on a lattice
This explorable illustrates beautiful dynamical patterns that can be generated by a simple game theoretic model on a lattice. The core of the model is the Prisoner’s Dilemma, a legendary game analyzed in game theory. In the game, two players can choose to cooperate or defect. Depending on their choice, they receive a pre-specified payoffs. The payoffs are chosen such that it seems difficult to make the right strategy choice.
“The walking head”
Pedestrian dynamics
This explorable illustrates how a remarkably simple mathematical model for pedestrian dynamics can capture a number of features that are observed in actual pedestrian flows on walkways for example. In the model individual pedestrians move with an individual anticipated speed and direction. When obstacles get in their way, either physical obstacles or other pedestrians, walkers experience a repulsive social force, that alters their velocity and current direction to avoid collision. This alone is sufficient to produce a variety of patterns that are reminiscent of actual pedestrian dynamics. The explorable is a simplified variant of a series of beautiful models introduced by Dirk Helbing that have found a wide range of application, e.g. panic dynamics, crowd turbulence, traffic jams and more.
“Clustershuck”
A network growth model that naturally yields clusters and heterogeneity
This explorable illustrates how strong heterogeneities, cluster-like structures and high variability in node connectivities can naturally emerge in growing networks. The mechanism explored here is very simple: When a new node is added to the network it picks another target node at random. Instead of linking to it, the new node establishes a link to one of the target’s neighbors.
“Thrilling Milling Schelling Herings”
Swarming behavior of animals that seek their kin
This explorables is a combination of two models, one that explains the emergence of dynamic patterns and collective behavior in schools of fish or flocks of birds, the second, the Schelling model, captures the geographic segregation of populations of different kinds of individuals. When these two models are combined, a great variety of beautiful dynamic swarming patterns can be generated. These patterns show traces of the generic swarming states like “milling” and segregation effects within these dynamic states.
“T. Schelling plays Go”
The Schelling model
This explorable illustrates the dynamics of the Schelling model named after economist and Nobel laureate Thomas Schelling (1921-2016). Although this model has been applied in different contexts, it is best known for its ability to capture geographical ethnic segregation of human populations and cities based on very simple principles.
“Nah dah dah nah nah... (Opus, 1984)”
Conway's Game of Life
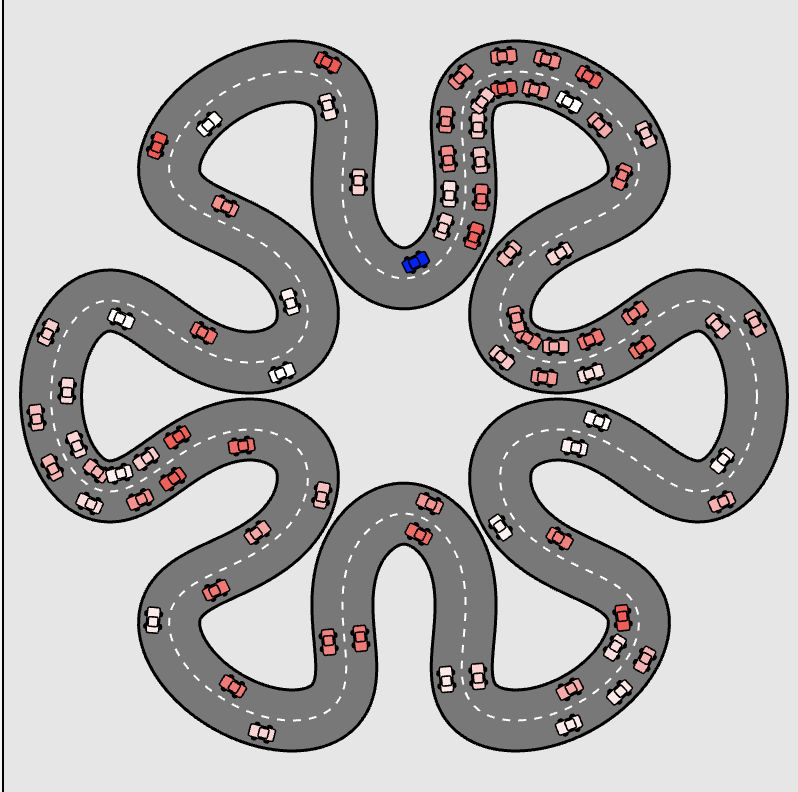
“Berlin 8:00 a.m.”
The emergence of phantom traffic jams
This explorable features an agent based model for road traffic and congestion. The model captures a phenomenon that most of us have witnessed on highways: phantom traffic jams, also known as traffic shocks or ghost jams. These are spontaneously emergent congested segments that move slowly and oppositely to the traffic. The explorable illustrates that phantom jams are more likely to occur if the variability in car speeds is higher:
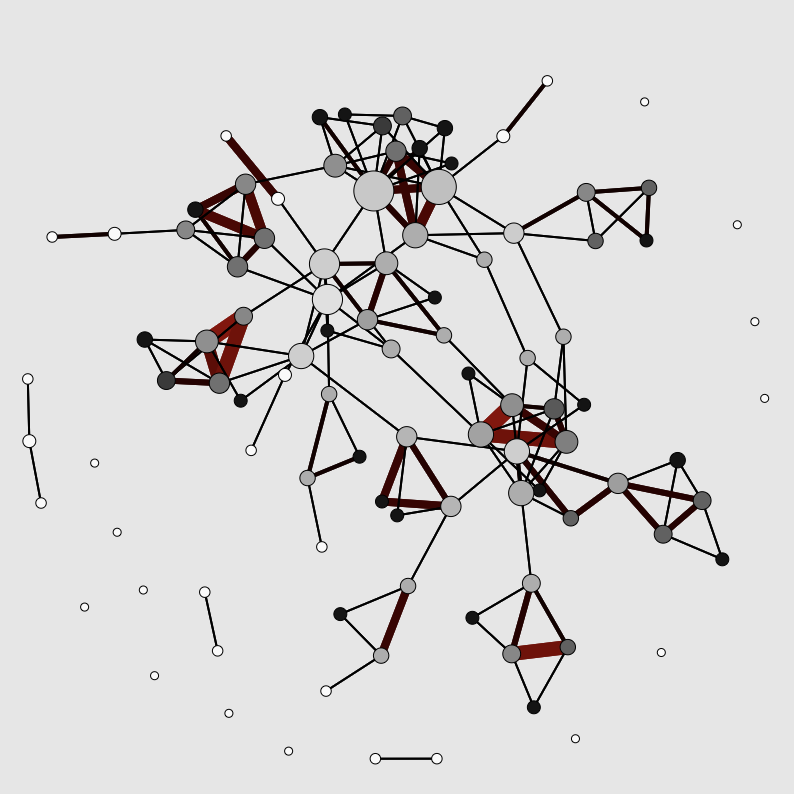
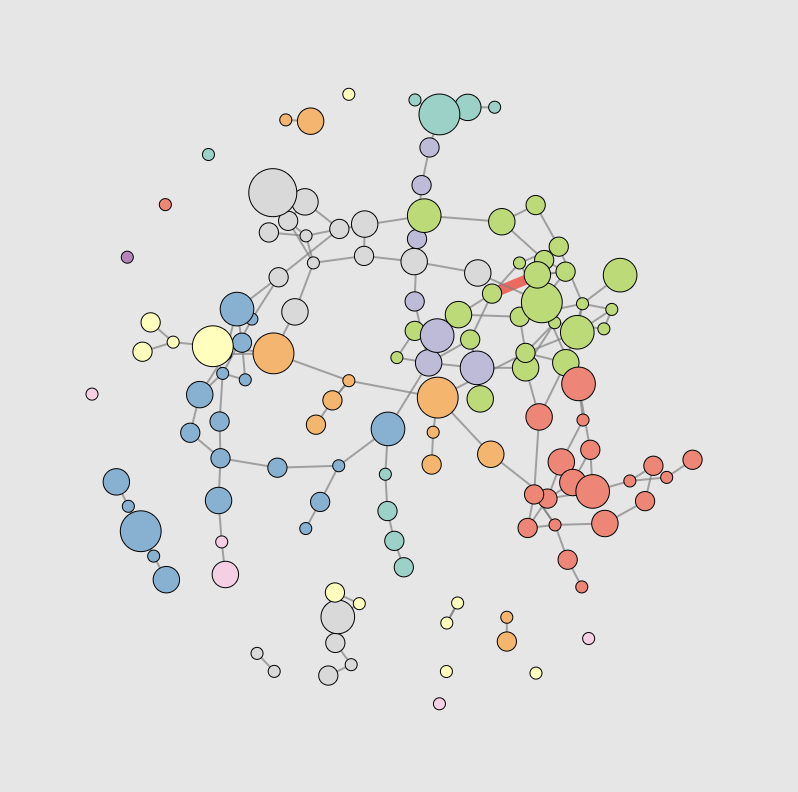
“Jujujajáki networks”
The emergence of communities in weighted networks
This explorable illustrates a dynamic network model that was designed to capture the emergence of community structures, heterogeneities and clusters that are frequently observed in social networks. Clusters are characterized by a high probability that a person’s ‘friends are also friends’. In this model not only the connectivity evolves but also the strength of links between nodes. The model was orginally proposed by Jussi Kumpula, Jukka-Pekka Onnela, Jari Saramäki, János Kertész and Kimmo Kaski.
“I sing well-tempered”
The Ising Model
This explorable illustrates one of the most famous models in statistical mechanics: The Ising Model. The model is structurally very simple and captures the properties and dynamics of magnetic materials, such as ferromagnets. It is so general that it is also used to describe opinion dynamics in populations and collective behavior in animal groups.
“Facebooked Flu Shots”
Network vaccination
This explorable illustrates and compares three vaccination strategies in complex networks. In this type of model nodes are people and network links potential transmission paths. “Vaccination” then means that nodes are disconnected from the network because they can no longer acquire or transmit a disease. Vaccination thus effectively dilutes the network. Two strategies, A and B, are straightforward to understand. A third one, C, is a bit odd and counterintuitive at first glance:
“I herd you!”
How herd immunity works
This explorable illustrates the mechanism of herd immunity. When an infectious disease spreads in a population, an individual can be protected by a vaccine that delivers immunity. But there’s a greater good. Immunization not only projects the individual directly. The immunized person will also never transmit the disease to others, effectively reducing the likelihood that the disease can proliferate in the population. Because of this, a disease can be eradicated even if not the entire population is immunized. This population wide effect is known as herd immunity.
“Echo Chambers”
A model for opinion dynamics
This explorable illustrates a network model that captures how opinion dynamics might work in a population and how clusters of uniform opinion might naturally emerge from an initially random system. The model is a variant of a model introduced by P. Holme and M. Newman in a 2006 paper: Nonequilibrium phase transition in the coevolution of networks and opinions.
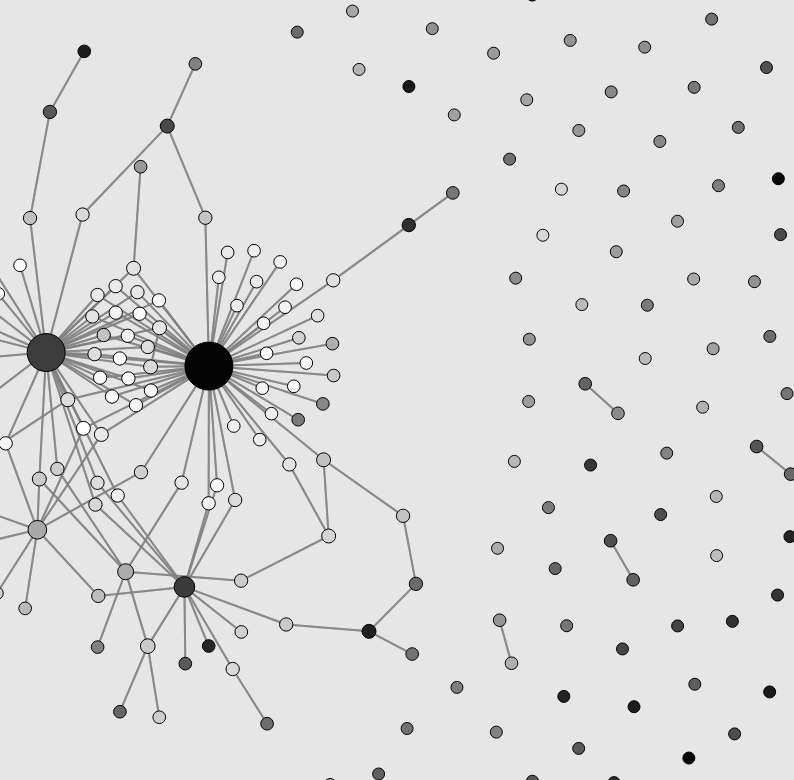
“Knitworks”
Growing complex networks
This explorable illustrates network growth based on preferential attachment, a variant of the Barabasi-Albert model that was introduced to capture strong heterogeneities observed in many natural and technological networks. It has become a popular model for scale-free networks in nature.
Preferential attachment means that nodes that enter the network during a growth process preferentially connect to nodes with specific properties. In the original system, they preferentially connect to existing nodes that are already well connected, increasing their connectivity even further. This rich get richer effect generates networks in which a few nodes are very strongly connected and very many nodes poorly.