“Horde of the Flies”
The Vicsek-Model
This explorable illustrates one of the most famous and most fundamental models for the emergence of flocking, swarming and synchronized behavior in animal groups. The model was originally published in a 1995 paper by Tamás Vicsek and co-workers and is therefore called the Vicsek-Model. The model can explain why transitions to flocking behavior in groups of animals are often not gradual. Instead, one can expect a sudden emergence of flocking and synchronized movements if a critical density is crossed.
“The walking head”
Pedestrian dynamics
This explorable illustrates how a remarkably simple mathematical model for pedestrian dynamics can capture a number of features that are observed in actual pedestrian flows on walkways for example. In the model individual pedestrians move with an individual anticipated speed and direction. When obstacles get in their way, either physical obstacles or other pedestrians, walkers experience a repulsive social force, that alters their velocity and current direction to avoid collision. This alone is sufficient to produce a variety of patterns that are reminiscent of actual pedestrian dynamics. The explorable is a simplified variant of a series of beautiful models introduced by Dirk Helbing that have found a wide range of application, e.g. panic dynamics, crowd turbulence, traffic jams and more.
“Eigenartig”
The spatial hypercycle model
This explorable illustrates the dynamics of the famous hypercycle model. It was originally conceived by Peter Schuster and Nobel laureate Manfred Eigen (1927-2019) in 1979 to investigate the chemical basis of the origin of life. Because living things make copies of themselves, in the beginning complex chemicals like polymer chains, including small RNA molecules (see e.g. RNA-world), had to acquire the ability to catalyse their own synthesis from smaller parts, e.g. single nucleotides.
“Nah dah dah nah nah... (Opus, 1984)”
Conway's Game of Life
“Berlin 8:00 a.m.”
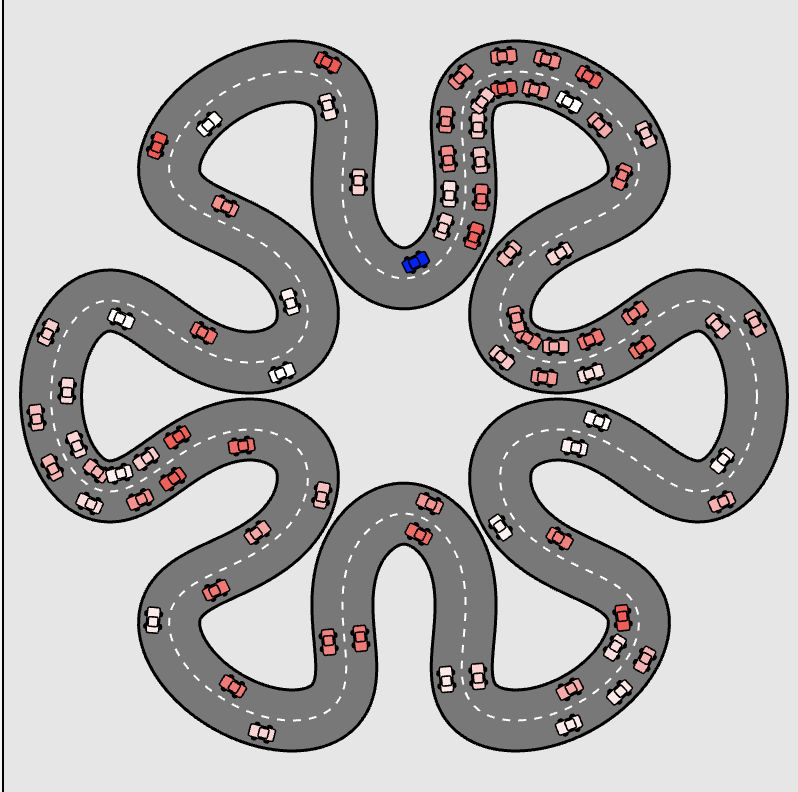
The emergence of phantom traffic jams
This explorable features an agent based model for road traffic and congestion. The model captures a phenomenon that most of us have witnessed on highways: phantom traffic jams, also known as traffic shocks or ghost jams. These are spontaneously emergent congested segments that move slowly and oppositely to the traffic. The explorable illustrates that phantom jams are more likely to occur if the variability in car speeds is higher:
“Jujujajáki networks”
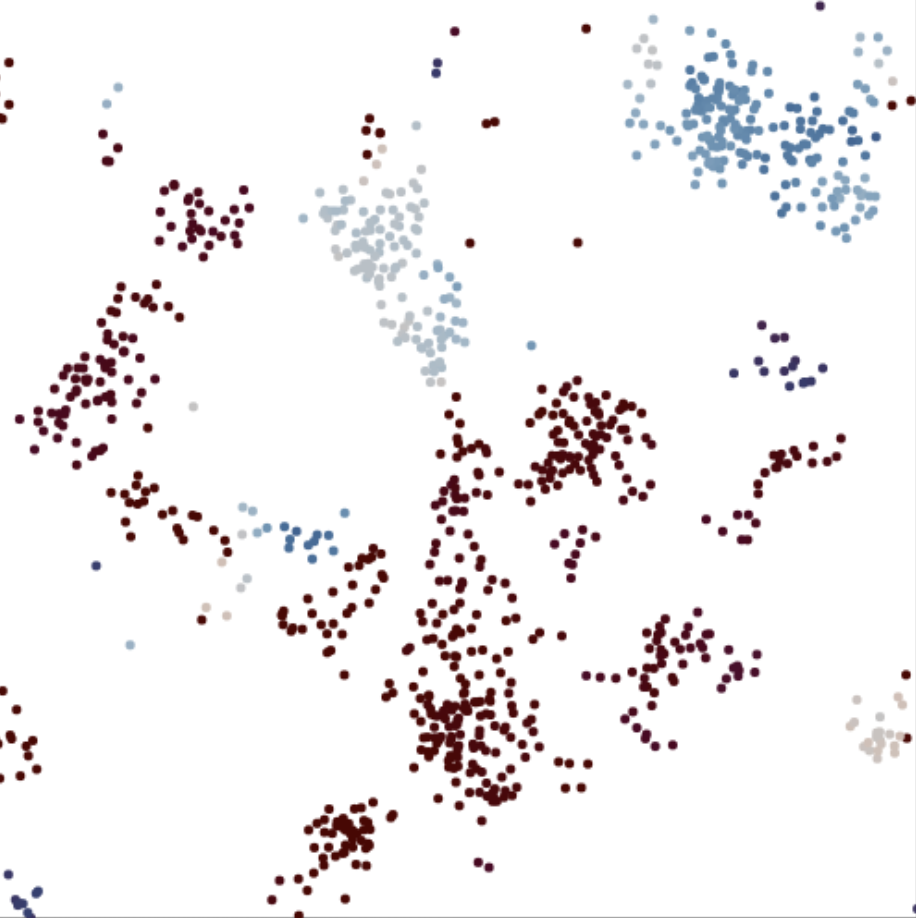
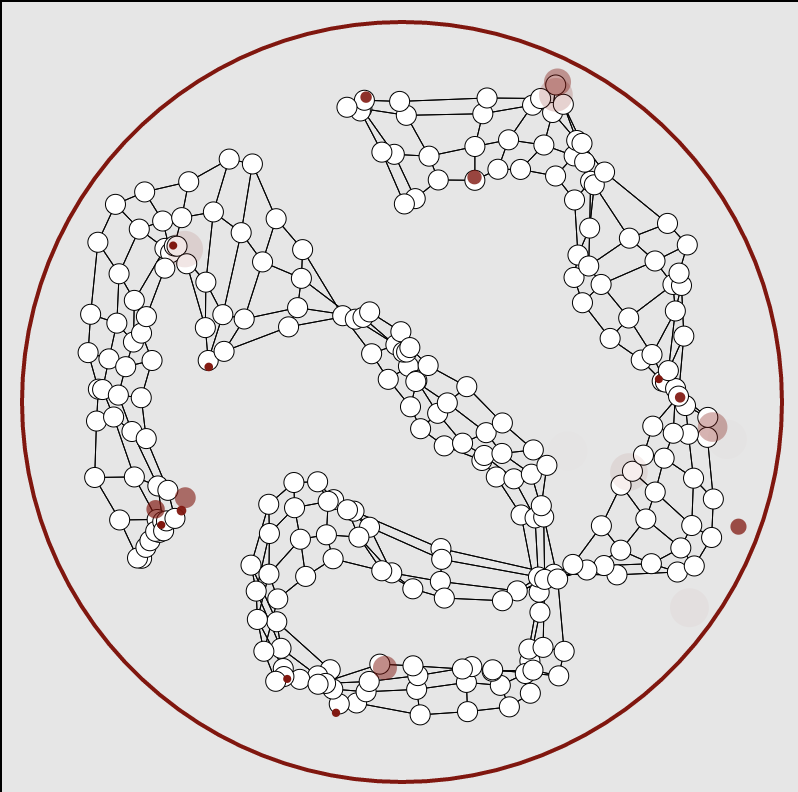
The emergence of communities in weighted networks
This explorable illustrates a dynamic network model that was designed to capture the emergence of community structures, heterogeneities and clusters that are frequently observed in social networks. Clusters are characterized by a high probability that a person’s ‘friends are also friends’. In this model not only the connectivity evolves but also the strength of links between nodes. The model was orginally proposed by Jussi Kumpula, Jukka-Pekka Onnela, Jari Saramäki, János Kertész and Kimmo Kaski.
“Hopfed Turingles”
Pattern Formation in a simple reaction-diffusion system
With this explorable you can discover a variety of spatio-temporal patterns that can be generated with a very famous and simple autocatalytic reaction diffusion system known as the Gray-Scott model. In the model two substances $U$ and $V$ interact and diffuse in a two-dimensional container. Although only two types of simple reactions occur, the system generates a wealth of different stable and dynamic spatio-temporal patterns depending on system parameters.
“Critically Inflammatory”
A forrest fire model
This explorable illustrates, as a representative of a broad range of dynamic phenomena, a simple model for the spatial spread of forest fires and the dynamic patterns they generate. In the model two antagonistic processes interplay, the reproductive growth of vegetation that continuously covers the landscape with trees susceptible to fires and spontaneously seeded (lightning strikes) forest fires that spread across areas of dense vegetation.
“Yo, Kohonen!”
Kohonen's Self-Organizing Map
This explorable illustrates the dynamics of a self-organizing map (SOM), specifically a neural network known as the Kohonen Map. The Kohonen map is a model for self-organization of biological neural networks and how the brain can learn to map signals from an input space, e.g. visual stimuli in the visual field, to a two dimensional layer of neurons, e.g. the visual cortex in the brain, in such a way that neighborhood properties in the stimulus space are conserved as best as possible: Neurons that are neighbors in the neural network should respond to stimuli that are also close in stimulus space.
“Knitworks”
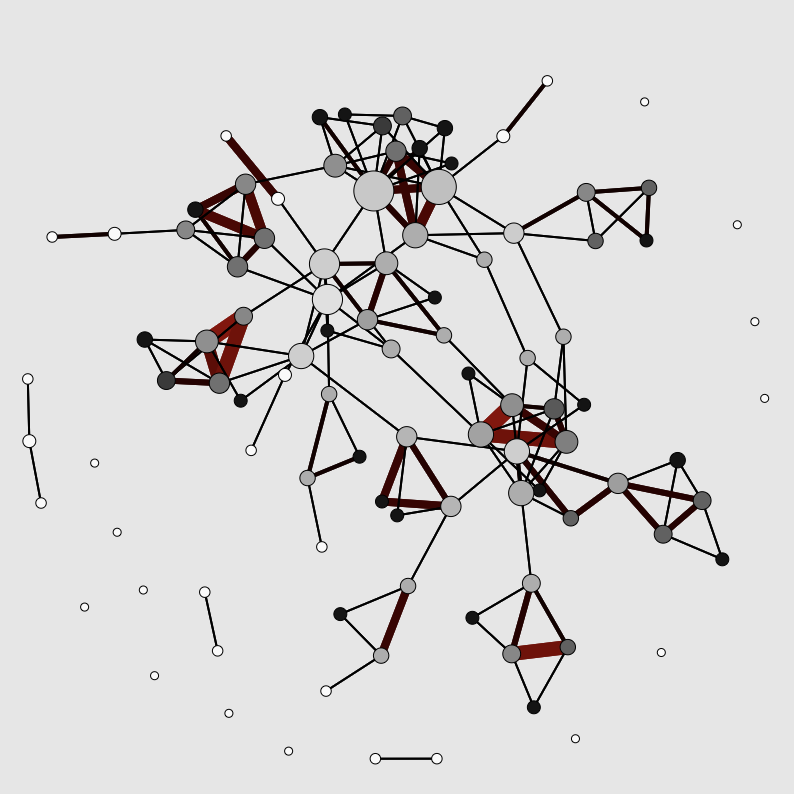
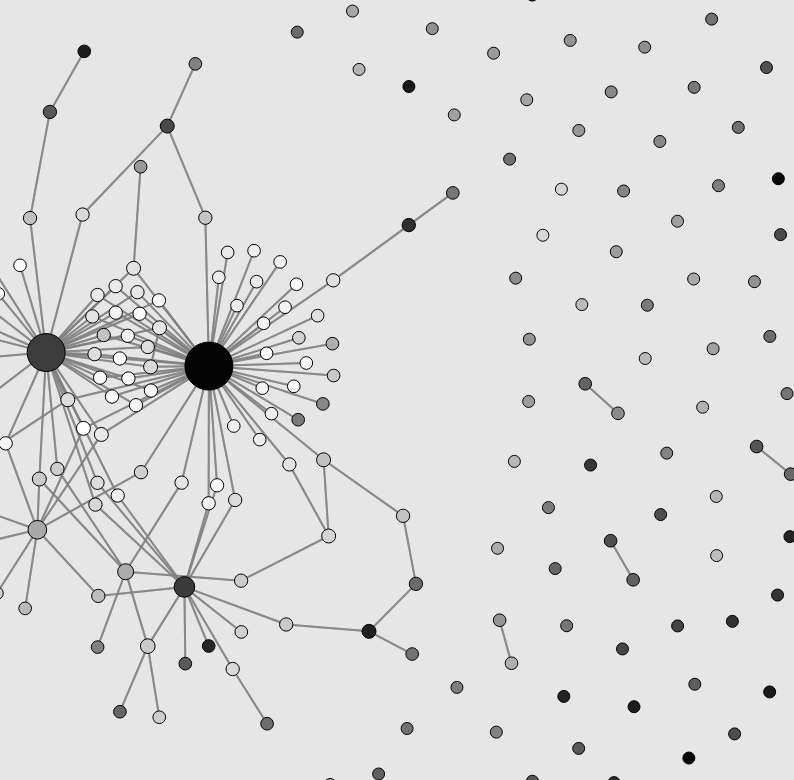
Growing complex networks
This explorable illustrates network growth based on preferential attachment, a variant of the Barabasi-Albert model that was introduced to capture strong heterogeneities observed in many natural and technological networks. It has become a popular model for scale-free networks in nature.
Preferential attachment means that nodes that enter the network during a growth process preferentially connect to nodes with specific properties. In the original system, they preferentially connect to existing nodes that are already well connected, increasing their connectivity even further. This rich get richer effect generates networks in which a few nodes are very strongly connected and very many nodes poorly.
“If you ask your XY”
The XY model of statistical mechanics
This explorable illustrates pattern formation and dynamics in the $XY$-model, an important model in statistical mechanics for studying phase-transitions and other phenomena. It’s a generalization of the famous Ising-Model. The $XY$-model is actually quite simple.
“Into the Dark”
Collective intelligence
This explorable illustrates how a school of fish can collectively find an optimal location, e.g. a dark, unexposed region in their environment simply by light-dependent speed control. The explorable is based on the model discussed in Flock’n Roll, which you may want to explore first.
“Flock'n Roll”
Collective behavior and swarming
This explorable illustrates of an intuitive dynamic model for collective motion (swarming) in animal groups. The model can be used to describe collective behavior observed in schooling fish or flocking birds, for example. The details of the model are described in a 2002 paper by Iain Couzin and colleagues.
“Particularly Stuck”
Diffusion Limited Aggregation
This explorable illustrates a process known as diffusion-limited aggregation (DLA). It’s a kinetic process driven by randomly diffusing particles that gives rise to fractal structures, reminiscent of things we see in natural systems. The process has been investigated in a number of scientific studies, e.g. the seminal paper by Witten & Sander.