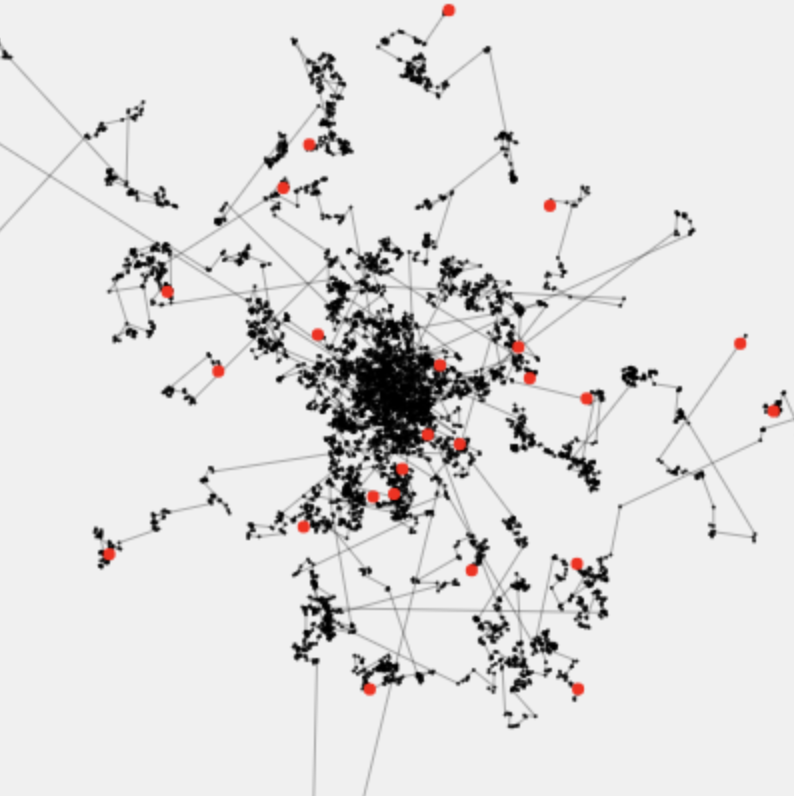
“Anomalous Itinerary”
Lévy flights
This explorable illustrates the properties of a class of random walks known as Lévy flights. To get the most out of this explorable, you may want to check out the explorable Albert & Carl Friedrich on ordinary random walks and diffusion first.
“Albert & Carl Friedrich”
Random Walks & Diffusion
This explorable illustrates the geometric and dynamic properties of the physical process of diffusion and its intimate relation to a mathematical object known as a random walk. It also illustrates graphically the implications of the central limit theorem that explains why we so often (normally) observe Gaussian distributions in nature. In the context of random walks this means that in the long run and from a great distance the paths of different types of walks become statistically indistiguishable.
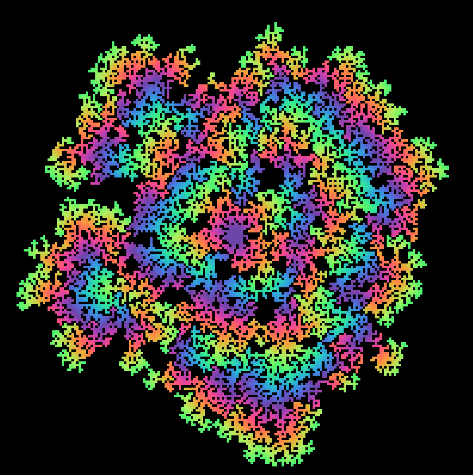
“Kelp!!!”
A stochastic cellular automaton
This explorable illustrates how fractal growth patterns can be generated by stochastic cellular automata. Cellular automata are spatially and temporally discrete dynamical systems that are conceptually very straightforward but can generate unexpected complex behavior, often fractal-like structures reminiscent of patterns we see in natural systems.
“Barista's Secret”
Percolation on a lattice
This explorable illustrates a process known as percolation. Percolation is a topic very important for understanding processes in physics, biology, geology, hydrology, horstology, epidemiology, and other fields. Percolation theory is the mathematical tool designed for understanding these processes.
“Critical HexSIRSize”
The stochastic, spatial SIRS model
This explorable illustrates the behavior of a contagion process near its critical point. Contagion processes, for example transmissible infectious diseases, typically exhibit a critical point, a threshold below which the disease will die out, and above which the disease is sustained in a population. Interesting dynamical things happen when the system is near its critical point.